Mi Teorema Favorito

Publicado: el 5 octubre, 2021 por AdminKonrad / Konrad Lorenz
Si un día alguien te pregunta ¿cuál es tu postre favorito?, seguramente ya estás pensando en una respuesta, ¿cierto? Pero si llegase alguien a preguntarte ¿cuál es tu teorema favorito?, ¿también tendrías la respuesta? Probablemente no. Y es que, en la vida de un matemático, inclusive para un estudiante de matemáticas (o de un área que las aplique), que vive utilizando una buena cantidad de teoremas, esta puede ser una cuestión que tal vez a hoy, no tenga respuesta.
Y fue esta pregunta tan simple y compleja a la vez, el personaje estrella en la celebración del cumpleaños número 23 del Programa de Matemáticas de la Fundación Universitaria Konrad Lorenz, evento realizado el 23 de agosto de 2021, que contó con el liderazgo del Docente Alexander Arredondo, las intervenciones de Guillermo Mantilla (docente del programa), Leidy Sánchez (estudiante), Julián Jiménez (graduado) y la participación especial de tres profesores invitados: Camilo Ramírez (antiguo docente del programa, actualmente docente en la Universidad Nacional de Colombia), Andrés Rivera (Universidad Javeriana sede Cali) y Jesús Muciño (Centro de Ciencias Matemáticas UNAM, Morelia, México). Todos ellos presentaron e hicieron un acercamiento a su teorema favorito, además de exponer las razones por las cuales eligieron ese teorema para los estudiantes y docentes asistentes.
Cuando recibí la invitación, tenía en mente tres teoremas que para mí entran en el ranking de mis teoremas favoritos, pero ¡tenía que decidirme por uno solo! Así que para que comprendan por qué el teorema que verán a continuación ocupa el número uno de la lista, hablaremos un poco de Química. Aquí vamos.
Todos hemos tenido acercamiento con moléculas, por nombrar algunas experiencias, cuando nos bañamos tenemos contacto con el agua, o cuando vamos a cocinar, usamos el cloruro de sodio (o mejor conocido como la sal de cocina) para enriquecer el sabor de nuestras preparaciones. El agua y el cloruro de sodio son moléculas. Hablemos del agua, para las mentes más curiosas, quizás en algún momento se hicieron la pregunta ¿de qué está compuesto el agua? Por su nomenclatura química H2O, se puede observar que el agua está compuesta por la unión de dos átomos de hidrógeno (H2) y uno de oxígeno (O). Los átomos son considerados como la unidad de materia más pequeña que existe, de modo que, si nos preguntásemos por quién o quiénes conforman el hidrógeno y/o el oxígeno, o en general, cualquier átomo, no tendría sentido, pues si los átomos son la unidad de materia más pequeña, sería contradictorio que exista una unidad menor.
Llegados a este punto, somos conscientes de que todo lo que tiene materia está formado por átomos, los cuales forman moléculas, y estas a su vez forman compuestos químicos, y así sucesivamente van formando todo lo que vemos a nuestro alrededor. Ahora, la pregunta que nos interesa es ¿será que en el mundo de las Matemáticas existen “los átomos de las Matemáticas”?
Pensemos en el número, quien será nuestra molécula y preguntémonos ¿qué números naturales componen ese número? Así como las moléculas están compuestas por la unión de átomos, en nuestro mundo matemático relacionaremos esa unión con una operación matemática, la multiplicación.
En ese orden de ideas, pensemos en números que multiplicados entre ellos nos den 28. 4 y 7 son un buen ejemplo, porque para nadie es un secreto que 4x7 = 28. ¿Será que podemos encontrar números que multiplicados entre ellos den 4? Pues resulta que 4 puede ser representado como 2 multiplicado por 2, así que, para nuestro ejemplo, 4 sigue siendo una molécula porque puede ser representado por medio de otro número, el 2. Por el momento tenemos el siguiente esquema:
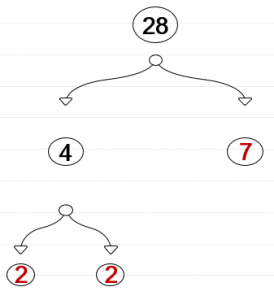
Si hacemos el mismo cuestionamiento para el 2 y el 7, ¿será que podemos encontrar números que multiplicados entre ellos den 2?, ¿será posible para el 7? Resulta que no. No existen números naturales que multiplicados entre sí den como resultado 2 ni 7. Si hacemos una analogía con los átomos, donde habíamos dicho que a los átomos no los compone nada porque ellos son la unidad de materia más pequeña, fijémonos que acá pasa exactamente lo mismo, tanto el 2 como el 7 no están compuestos por algo más, ellos son los átomos que conforman la molécula 28, de modo que 28 puede ser escrito como 28 = 2x2x7. Además, 2 y 7 son números muy especiales porque ellos son números primos.
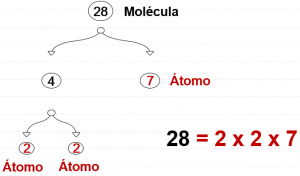
De este modo podemos decir que, así como las moléculas son uniones de átomos, los números naturales son productos de números primos. Así como las moléculas están compuestas por átomos, los números naturales están compuestos por números primos. Así como los átomos conforman todo lo que vemos a nuestro alrededor, entonces ¡los números primos juegan el mismo papel en las Matemáticas!
Y ahora que estamos ante un resultado de alto impacto para el mundo matemático, les presento mi teorema favorito:

Notemos que hay unas palabras resaltadas en rojo, precisamente porque cuando dice que:
- TODOS: hace referencia a todos los números naturales del universo matemático.
- PUEDE EXPRESARSE: nos asegura que puede representarse, aunque no nos dice cómo.
- FORMA ÚNICA: teniendo una representación con números primos que, multiplicados entre sí, dé como resultado un número natural, no existe otra representación de producto de primos diferentes que den como resultado ese mismo número natural.
La trascendencia de los números primos en las Matemáticas es gigantesca, por lo que merecen toda nuestra atención y este teorema condensa esta trascendencia en un enunciado tan sencillo pero complejo a la vez. De hecho, no somos conscientes de ello, pero, es este el primer teorema que nos enseñan en la escuela (y no el Teorema de Pitágoras, que seguramente lo recordamos muy bien), cuando nos enseñan a factorizar, a calcular el Máximo Común Divisor o el Mínimo Común Múltiplo, estamos ante resultados del Teorema Fundamental de la Aritmética. Y por nombrar, entre otras aplicaciones de este fastuoso teorema, existen métodos de codificación que aprovechan el Teorema Fundamental de la Aritmética, para utilizar números con gran cantidad de cifras tales que sean compuestos por el producto de números primos con más de 1.000 cifras, porque hoy en día existe una probabilidad muy grande de que no se logre encontrar esos números primos que conforman dicho número compuesto.
Por estas y muchas otras razones, el Teorema Fundamental de la Aritmética ocupa el lugar más especial en mi lista de teoremas favoritos.
Leidy Catherinne Sánchez Ascanio
Estudiante de matemáticas.




